Khan Academy on a Stick
Surface integrals and Stokes' theorem
Parameterizing a surface. Surface integrals. Stokes' theorem.
-
 Introduction to Parametrizing a Surface with Two Parameters
cc
Introduction to Parametrizing a Surface with Two Parameters
ccIntroduction to Parametrizing a Surface with Two Parameters
-
 Determining a Position Vector-Valued Function for a Parametrization of Two Parameters
cc
Determining a Position Vector-Valued Function for a Parametrization of Two Parameters
ccDetermining a Position Vector-Valued Function for a Parametrization of Two Parameters
Parameterizing a surface
You can parameterize a line with a position vector valued function and understand what a differential means in that context already. This tutorial will take things further by parametrizing surfaces (2 parameters baby!) and have us thinking about partial differentials.
-
 Partial Derivatives of Vector-Valued Functions
cc
Partial Derivatives of Vector-Valued Functions
ccPartial Derivatives of Vector-Valued Functions
-
 Introduction to the Surface Integral
cc
Introduction to the Surface Integral
ccIntroduction to the surface integral
-
 Example of calculating a surface integral part 1
cc
Example of calculating a surface integral part 1
ccExample of calculating a surface integral part 1
-
 Example of calculating a surface integral part 2
cc
Example of calculating a surface integral part 2
ccExample of calculating a surface integral part 2
-
 Example of calculating a surface integral part 3
cc
Example of calculating a surface integral part 3
ccExample of calculating a surface integral part 3
-
 Surface Integral Example Part 1 - Parameterizing the Unit Sphere
cc
Surface Integral Example Part 1 - Parameterizing the Unit Sphere
ccVisualizing a suitable parameterization
-
 Surface Integral Example Part 2 - Calculating the Surface Differential
cc
Surface Integral Example Part 2 - Calculating the Surface Differential
ccTaking the cross product to calculate the surface differential in terms of the parameters
-
 Surface Integral Example Part 3 - The Home Stretch
cc
Surface Integral Example Part 3 - The Home Stretch
ccUsing a few trigonometric identities to finally calculate the value of the surface integral
-
 Surface Integral Ex2 part 1 - Parameterizing the Surface
cc
Surface Integral Ex2 part 1 - Parameterizing the Surface
ccParametrizing a surface that can be explictly made a function of x and y.
-
 Surface Integral Ex2 part 2 - Evaluating Integral
cc
Surface Integral Ex2 part 2 - Evaluating Integral
ccEvaluating the surface integral
-
 Surface Integral Ex3 part 1 - Parameterizing the Outside Surface
Surface Integral Ex3 part 1 - Parameterizing the Outside Surface
Breaking apart a larger surface into its components
-
 Surface Integral Ex3 part 2 - Evaluating the Outside Surface
Surface Integral Ex3 part 2 - Evaluating the Outside Surface
Evaluating the surface integral over the outside of the chopped cylinder
-
 Surface Integral Ex3 part 3 - Top surface
cc
Surface Integral Ex3 part 3 - Top surface
ccParametrizing the top surface
-
 Surface Integral Ex3 part 4 - Home Stretch
Surface Integral Ex3 part 4 - Home Stretch
Evaluating the third surface integral and coming to the final answer
Surface integrals
Finding line integrals to be a bit boring? Well, this tutorial will add new dimension to your life by explore what surface integrals are and how we can calculate them.
-
 Conceptual Understanding of Flux in Three Dimensions
cc
Conceptual Understanding of Flux in Three Dimensions
ccConceptual understanding of flux across a two-dimensional surface
-
 Constructing a unit normal vector to a surface
cc
Constructing a unit normal vector to a surface
ccDeriving a unit normal vector from the surface parametrization
-
 Vector representation of a Surface Integral
cc
Vector representation of a Surface Integral
ccDifferent ways of representing a flux integral
Flux in 3-D and constructing unit normal vectors to surface
Flux can be view as the rate at which "stuff" passes through a surface. Imagine a next placed in a river and imagine the water that is flowing directly across the net in a unit of time--this is flux (and it would depend on the orientation of the net, the shape of the net, and the speed and direction of the current). It is an important idea throughout physics and is key for understanding Stokes' theorem and the divergence theorem.
-
 Stokes' Theorem Intuition
Stokes' Theorem Intuition
Conceptual understanding of why the curl of a vector field along a surface would relate to the line integral around the surface's boundary
-
 Green's and Stokes' Theorem Relationship
Green's and Stokes' Theorem Relationship
Seeing that Green's Theorem is just a special case of Stokes' Theorem
-
 Orienting Boundary with Surface
Orienting Boundary with Surface
Determining the proper orientation of the boundary given the orientation of the surface
-
 Orientation and Stokes
Orientation and Stokes
Determining the proper orientation of a boundary given the orientation of the normal vector
-
 Conditions for Stokes Theorem
cc
Conditions for Stokes Theorem
ccUnderstanding when you can use Stokes. Piecewise-smooth lines and surfaces
-
 Stokes Example Part 1
cc
Stokes Example Part 1
ccStarting to apply Stokes theorem to solve a line integral
-
 Part 2 Parameterizing the Surface
Part 2 Parameterizing the Surface
-
 Stokes Example Part 3 - Surface to Double Integral
Stokes Example Part 3 - Surface to Double Integral
Converting the surface integral to a double integral
-
 Stokes Example Part 4 - Curl and Final Answer
cc
Stokes Example Part 4 - Curl and Final Answer
ccFinding the curl of the vector field and then evaluating the double integral in the parameter domain
-
 Evaluating Line Integral Directly - Part 1
Evaluating Line Integral Directly - Part 1
Showing that we didn't need to use Stokes' Theorem to evaluate this line integral
-
 Evaluating Line Integral Directly - Part 2
Evaluating Line Integral Directly - Part 2
Finishing up the line integral with a little trigonometric integration
Stokes' theorem intuition and application
Stokes' theorem relates the line integral around a surface to the curl on the surface. This tutorial explores the intuition behind Stokes' theorem, how it is an extension of Green's theorem to surfaces (as opposed to just regions) and gives some examples using it. We prove Stokes' theorem in another tutorial. Good to come to this tutorial having experienced the tutorial on "flux in 3D".
-
 Stokes' Theorem Proof Part 1
cc
Stokes' Theorem Proof Part 1
ccThe beginning of a proof of Stokes' theorem for a special class of surfaces. Finding the curl of our vector field.
-
 Stokes' Theorem Proof Part 2
Stokes' Theorem Proof Part 2
Figuring out a parameterization of our surface and representing dS
-
 Stokes' Theorem Proof Part 3
Stokes' Theorem Proof Part 3
Writing our surface integral as a double integral over the domain of our parameters
-
 Stokes' Theorem Proof Part 4
Stokes' Theorem Proof Part 4
Starting to work on the line integral about the surface
-
 Stokes' Theorem Proof Part 5
Stokes' Theorem Proof Part 5
Working on the integrals...
-
 Stokes' Theorem Proof Part 6
Stokes' Theorem Proof Part 6
More manipulating the integrals...
-
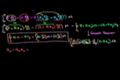 Stokes' Theorem Proof Part 7
Stokes' Theorem Proof Part 7
Using Green's Theorem to complete the proof
Proof of Stokes' theorem
You know what Stokes' theorem is and how to apply it, but are craving for some real proof that it is true. Well, you've found the right tutorial!