Khan Academy on a Stick : Laplace transform

Khan Academy on a Stick

Differential equations

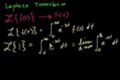Laplace Transform 1
cc

Introduction to the Laplace Transform
Laplace Transform 2
cc

Laplace transform of e^at
L{sin(at)}) - transform of sin(at)
cc

Laplace Transform of sin(at) (part 1)
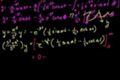Part 2 of the transform of the sin(at)
cc

Part 2 of getting the Laplace transform of sin(at)

Laplace transform

We now use one of the coolest techniques in mathematics to transform differential equations into algebraic ones. You'll also learn about transforms in general!

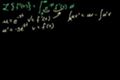Laplace as linear operator and Laplace of derivatives
cc

Useful properties of the Laplace Transform
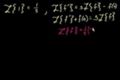Laplace Transform of cos t and polynomials
cc

Laplace transform of cosine and polynomials!
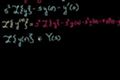"Shifting" transform by multiplying function by exponential
cc

A grab bag of things to know about the Laplace Transform.
Laplace Transform of : L{t}
cc

Determining the Laplace Transform of t
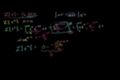Laplace Transform of t^n: L{t^n}
cc

Laplace Transform of t^n: L{t^n}
Laplace Transform of the Unit Step Function
cc

Introduction to the unit step function and its Laplace Transform
Inverse Laplace Examples
cc

Using our toolkit to take some inverse Laplace Transforms
Dirac Delta Function
cc

Introduction to the Dirac Delta Function
Laplace Transform of the Dirac Delta Function
cc

Figuring out the Laplace Transform of the Dirac Delta Function

Properties of the Laplace transform

You know how to use the definition of the Laplace transform. In this tutorial, we'll explore some of the properties of the transform that will start to make it clear why they are so useful for differential equations. This tutorial is paired well with the tutorial on using the "Laplace transform to solve differential equations". In fact you might come back to this tutorial over and over as you solve more and more problems.

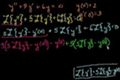Laplace Transform to solve an equation
cc

Using the Laplace Transform to solve an equation we already knew how to solve.
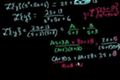Laplace Transform solves an equation 2
cc

Second part of using the Laplace Transform to solve a differential equation.
Using the Laplace Transform to solve a nonhomogeneous eq
cc

Solving a non-homogeneous differential equation using the Laplace Transform
Laplace/Step Function Differential Equation
cc

Hairy differential equation involving a step function that we use the Laplace Transform to solve.

Laplace transform to solve a differential equation

You know a good bit about taking Laplace transform and useful properties of the transform. You are dying to actually apply these skills to an actual differential equation. Wait no longer!

Introduction to the Convolution
cc

Introduction to the Convolution
The Convolution and the Laplace Transform
cc

Understanding how the product of the Transforms of two functions relates to their convolution.
Using the Convolution Theorem to Solve an Initial Value Prob
cc

Using the Convolution Theorem to solve an initial value problem

The convolution integral

This tutorial won't be as convoluted as you might suspect. We'll see what multiplying transforms in the s-domain give us in the time domain.