Khan Academy on a Stick
Inferential statistics
Making inferences based on sample data. Confidence intervals. Margin of error. Hypothesis testing.
-
 Introduction to the Normal Distribution
cc
Introduction to the Normal Distribution
ccExploring the normal distribution
-
 Normal Distribution Excel Exercise
cc
Normal Distribution Excel Exercise
cc(Long-26 minutes) Presentation on spreadsheet to show that the normal distribution approximates the binomial distribution for a large number of trials.
-
 ck12.org Normal Distribution Problems: Qualitative sense of normal distributions
cc
ck12.org Normal Distribution Problems: Qualitative sense of normal distributions
ccDiscussion of how "normal" a distribution might be
-
 ck12.org Normal Distribution Problems: Empirical Rule
cc
ck12.org Normal Distribution Problems: Empirical Rule
ccUsing the empirical rule (or 68-95-99.7 rule) to estimate probabilities for normal distributions
-
 ck12.org Normal Distribution Problems: z-score
cc
ck12.org Normal Distribution Problems: z-score
ccZ-score practice
-
 ck12.org Exercise: Standard Normal Distribution and the Empirical Rule
cc
ck12.org Exercise: Standard Normal Distribution and the Empirical Rule
ccUsing the Empirical Rule with a standard normal distribution
-
 ck12.org: More Empirical Rule and Z-score practice
cc
ck12.org: More Empirical Rule and Z-score practice
ccMore Empirical Rule and Z-score practice
Normal distribution
The normal distribution (often referred to as the "bell curve" is at the core of most of inferential statistics. By assuming that most complex processes result in a normal distribution (we'll see why this is reasonable), we can gauge the probability of it happening by chance. To best enjoy this tutorial, it is good to come to it understanding what probability distributions and random variables are. You should also be very familiar with the notions of population and sample mean and standard deviation.
-
 Central Limit Theorem
cc
Central Limit Theorem
ccIntroduction to the central limit theorem and the sampling distribution of the mean
-
 Sampling Distribution of the Sample Mean
cc
Sampling Distribution of the Sample Mean
ccThe central limit theorem and the sampling distribution of the sample mean
-
 Sampling Distribution of the Sample Mean 2
cc
Sampling Distribution of the Sample Mean 2
ccMore on the Central Limit Theorem and the Sampling Distribution of the Sample Mean
-
 Standard Error of the Mean
cc
Standard Error of the Mean
ccStandard Error of the Mean (a.k.a. the standard deviation of the sampling distribution of the sample mean!)
-
 Sampling Distribution Example Problem
cc
Sampling Distribution Example Problem
ccFiguring out the probability of running out of water on a camping trip
Sampling distribution
In this tutorial, we experience one of the most exciting ideas in statistics--the central limit theorem. Without it, it would be a lot harder to make any inferences about population parameters given sample statistics. It tells us that, regardless of what the population distribution looks like, the distribution of the sample means (you'll learn what that is) can be normal. Good idea to understand a bit about normal distributions before diving into this tutorial.
-
 Confidence Interval 1
cc
Confidence Interval 1
ccEstimating the probability that the true population mean lies within a range around a sample mean.
-
 Confidence Interval Example
cc
Confidence Interval Example
ccConfidence Interval Example
-
 Small Sample Size Confidence Intervals
cc
Small Sample Size Confidence Intervals
ccConstructing small sample size confidence intervals using t-distributions
Confidence intervals
We all have confidence intervals ("I'm the king of the world!!!!") and non-confidence intervals ("No one loves me"). That is not what this tutorial is about. This tutorial takes what you already know about the central limit theorem, sampling distributions, and z-scores and uses these tools to dive into the world of inferential statistics. It may seem magical at first, but from our sample, we can now make inferences about the probability of our population mean actually being in an interval.
-
 Mean and Variance of Bernoulli Distribution Example
cc
Mean and Variance of Bernoulli Distribution Example
ccMean and Variance of Bernoulli Distribution Example
-
 Bernoulli Distribution Mean and Variance Formulas
cc
Bernoulli Distribution Mean and Variance Formulas
ccBernoulli Distribution Mean and Variance Formulas
-
 Margin of Error 1
cc
Margin of Error 1
ccFinding the 95% confidence interval for the proportion of a population voting for a candidate.
-
 Margin of Error 2
cc
Margin of Error 2
ccFinding the 95% confidence interval for the proportion of a population voting for a candidate.
Bernoulli distributions and margin of error
Ever wondered what pollsters are talking about when they said that there is a 3% "margin of error" in their results. Well, this tutorial will not only explain what it means, but give you the tools and understanding to be a pollster yourself!
-
 Hypothesis Testing and P-values
cc
Hypothesis Testing and P-values
ccHypothesis Testing and P-values
-
 One-Tailed and Two-Tailed Tests
cc
One-Tailed and Two-Tailed Tests
ccOne-Tailed and Two-Tailed Tests
-
 Type 1 Errors
cc
Type 1 Errors
ccType 1 Errors
-
 Z-statistics vs. T-statistics
cc
Z-statistics vs. T-statistics
ccZ-statistics vs. T-statistics
-
 Small Sample Hypothesis Test
cc
Small Sample Hypothesis Test
ccSmall Sample Hypothesis Test
-
 T-Statistic Confidence Interval
cc
T-Statistic Confidence Interval
ccT-Statistic Confidence Interval (for small sample sizes)
-
 Large Sample Proportion Hypothesis Testing
cc
Large Sample Proportion Hypothesis Testing
ccLarge Sample Proportion Hypothesis Testing
Hypothesis testing with one sample
This tutorial helps us answer one of the most important questions not only in statistics, but all of science: how confident are we that a result from a new drug or process is not due to random chance but due to an actual impact. If you are familiar with sampling distributions and confidence intervals, you're ready for this adventure!
-
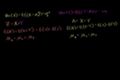 Variance of Differences of Random Variables
cc
Variance of Differences of Random Variables
ccVariance of Differences of Random Variables
-
 Difference of Sample Means Distribution
cc
Difference of Sample Means Distribution
ccDifference of Sample Means Distribution
-
 Confidence Interval of Difference of Means
cc
Confidence Interval of Difference of Means
ccConfidence Interval of Difference of Means
-
 Clarification of Confidence Interval of Difference of Means
cc
Clarification of Confidence Interval of Difference of Means
ccClarification of Confidence Interval of Difference of Means
-
 Hypothesis Test for Difference of Means
cc
Hypothesis Test for Difference of Means
ccHypothesis Test for Difference of Means
-
 Comparing Population Proportions 1
cc
Comparing Population Proportions 1
ccComparing Population Proportions 1
-
 Comparing Population Proportions 2
cc
Comparing Population Proportions 2
ccComparing Population Proportions 2
-
 Hypothesis Test Comparing Population Proportions
cc
Hypothesis Test Comparing Population Proportions
ccHypothesis Test Comparing Population Proportions
Hypothesis testing with two samples
You're already familiar with hypothesis testing with one sample. In this tutorial, we'll go further by testing whether the difference between the means of two samples seems to be unlikely purely due to chance.
-
 Chi-Square Distribution Introduction
cc
Chi-Square Distribution Introduction
ccChi-Square Distribution Introduction
-
 Pearson's Chi Square Test (Goodness of Fit)
cc
Pearson's Chi Square Test (Goodness of Fit)
ccPearson's Chi Square Test (Goodness of Fit)
-
 Contingency Table Chi-Square Test
cc
Contingency Table Chi-Square Test
ccContingency Table Chi-Square Test
Chi-square probability distribution
You've gotten good at hypothesis testing when you can make assumptions about the underlying distributions. In this tutorial, we'll learn about a new distribution (the chi-square one) and how it can help you (yes, you) infer what an underlying distribution even is!
-
 ANOVA 1 - Calculating SST (Total Sum of Squares)
cc
ANOVA 1 - Calculating SST (Total Sum of Squares)
ccAnalysis of Variance 1 - Calculating SST (Total Sum of Squares)
-
 ANOVA 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi
cc
ANOVA 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi
ccAnalysis of Variance 2 - Calculating SSW and SSB (Total Sum of Squares Within and Between).avi
-
 ANOVA 3 -Hypothesis Test with F-Statistic
cc
ANOVA 3 -Hypothesis Test with F-Statistic
ccAnalysis of Variance 3 -Hypothesis Test with F-Statistic
Analysis of variance
You already know a good bit about hypothesis testing with one or two samples. Now we take things further by making inferences based on three or more samples. We'll use the very special F-distribution to do it (F stands for "fabulous").