Khan Academy on a Stick
Functions
Identifying, solving, and graphing various types of functions.
-
 What is a function
What is a function
-
 Difference between Equations and Functions
Difference between Equations and Functions
Jesse Roe and Sal talk about the difference between equations and functions
-
 Function example problems
cc
Function example problems
ccLinear Function Graphs
-
 Ex: Constructing a function
cc
Ex: Constructing a function
ccBasic Linear Function
-
 Understanding Function Notation Example 1)
cc
Understanding Function Notation Example 1)
cc -
 Understanding Function Notation Example 2)
cc
Understanding Function Notation Example 2)
cc -
 Understanding Function Notation Example 3)
Understanding Function Notation Example 3)
-
 Testing if a relationship is a function
cc
Testing if a relationship is a function
ccTesting if a relationship is a function
-
 Graphical Relations and Functions
cc
Graphical Relations and Functions
ccGraphical Relations and Functions
-
 Functions as Graphs
cc
Functions as Graphs
cc -
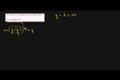 Recognizing functions (example 1)
Recognizing functions (example 1)
-
 Recognizing functions (example 2)
cc
Recognizing functions (example 2)
cc -
 Relations and Functions
cc
Relations and Functions
ccRelations and Functions
-
 Functional Relationships 1
cc
Functional Relationships 1
ccFunctional Relationships 1
-
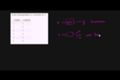 Recognizing functions (example 3)
cc
Recognizing functions (example 3)
cc -
 Recognizing functions (example 4)
Recognizing functions (example 4)
-
 Recognizing functions (example 5)
Recognizing functions (example 5)
Function introduction
Relationships can be any association between sets of numbers while functions have only one output for a given input. This tutorial works through a bunch of examples of testing whether something is a valid function. As always, we really encourage you to pause the videos and try the problems before Sal does!
-
 Domain of a function
cc
Domain of a function
ccFiguring out the domain of a function
-
 Domain and Range of a Relation
cc
Domain and Range of a Relation
ccDomain and Range of a Relation
-
 Domain and Range of a Function Given a Formula
cc
Domain and Range of a Function Given a Formula
ccDomain and Range of a Function Given a Formula
-
 Domain and Range 1
cc
Domain and Range 1
ccDomain and Range 1
-
 Domain of a Radical Function
cc
Domain of a Radical Function
ccDomain of a Radical Function
-
 Domain and Range 2
cc
Domain and Range 2
ccDomain and Range 2
-
 Domain and Range of a Function
cc
Domain and Range of a Function
cc
Domain and range
What values can you and can you not input into a function? What values can the function output? The domain is the set of values that the function is defined for (i.e., the values that you can input into a function). The range is the set of values that the function output can take on. This tutorial covers the ideas of domain and range through multiple worked examples. These are really important ideas as you study higher mathematics.
-
 Direct and Inverse Variation
cc
Direct and Inverse Variation
ccUnderstanding direct and inverse variation
-
 Recognizing Direct and Inverse Variation
cc
Recognizing Direct and Inverse Variation
ccExamples of variables varying directly and inversely
-
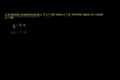 Proportionality Constant for Direct Variation
cc
Proportionality Constant for Direct Variation
ccProportionality Constant for Direct Variation
-
 Direct Variation Models
cc
Direct Variation Models
ccDirect Variation Models
-
 Direct Variation 1
cc
Direct Variation 1
ccDirect Variation 1
-
 Inverse Variation Application
cc
Inverse Variation Application
ccInverse Variation Application
-
 Direct Inverse and Joint Variation
cc
Direct Inverse and Joint Variation
ccDirect Inverse and Joint Variation
-
 Direct Variation Application
cc
Direct Variation Application
ccDirect Variation Application
Direct and inverse variation
Whether you are talking about how force relates to acceleration or how the cost of movie tickets relates to the number of people going, it is not uncommon in this universe for things to vary directly. Similarly, when you are, say, talking about how hunger might relate to seeing roadkill, things can vary inversely. This tutorial digs deeper into these ideas with a bunch of examples of direct and inverse variation.
-
 Ex 1: Evaluating a function
cc
Ex 1: Evaluating a function
ccEvaluating Functions
-
 Ex 2: Graphing a basic function
cc
Ex 2: Graphing a basic function
ccGraphing a Basic Function
-
 Graphing a parabola with a table of values
Graphing a parabola with a table of values
Graphing a parabola with a table of values
-
 Ex 4: Graphing radical functions
cc
Ex 4: Graphing radical functions
ccGraphing Radical Functions
-
 Ex: Graphing exponential functions
cc
Ex: Graphing exponential functions
ccGraphing Exponential Functions
Graphing functions
You've already graphed functions when you graphed lines and curves in other topics so this really isn't anything new. Now we'll do a few more examples in this tutorial, but we'll use the function notation to make things a bit more explicit.
-
 Quotient of Functions
cc
Quotient of Functions
ccQuotient of functions and factoring by grouping
-
 Sum of Functions
cc
Sum of Functions
ccSum of Functions
-
 Product of Functions
cc
Product of Functions
ccProduct of Functions
-
 Difference of Functions
cc
Difference of Functions
ccDifference of Functions
-
 Evaluating a function expression
cc
Evaluating a function expression
cc -
 Evaluating composite functions example
Evaluating composite functions example
Evaluating function expressions
This is a super fun tutorial where we'll evaluate expressions that involve functions. We'll add, subtract, multiply and divide them. We'll also do composite functions which involves taking the output of one function to be the input of another one! As always, pause the video and try the problem before Sal does!
-
 Introduction to Function Inverses
cc
Introduction to Function Inverses
ccIntroduction to Function Inverses
-
 Function Inverse Example 1
cc
Function Inverse Example 1
ccFunction Inverse Example 1
-
 Function Inverses Example 2
cc
Function Inverses Example 2
ccFunction Inverses Example 2
-
 Function Inverses Example 3
cc
Function Inverses Example 3
ccFunction Inverses Example 3
Function inverses
Functions associate a set of inputs with a set of outputs (in fancy language, they "map" one set to another). But can we go the other way around? Are there functions that can start with the outputs as inputs and produce the original inputs as outputs? Yes, there are! They are called function inverses! This tutorial works through a bunch of examples to get you familiar with the world of function inverses.
-
 New operator definitions
cc
New operator definitions
ccGetting comfortable with evaluating newly defined function operators
-
 New operator definitions 2
New operator definitions 2
Worked examples of working with newly defined operators
New operator definitions
Are you bored of the traditional operators of addition, subtraction, multiplication and division? Do even exponents seem a little run-of-the-mill? Well in this tutorial, we will--somewhat arbitrarily--define completely new operators and notation (which are essentially new function definitions without the function notation). Not only will this tutorial expand your mind, it could be the basis of a lot of fun at your next dinner party!
-
 Introduction to functions
cc
Introduction to functions
ccAn introduction to functions.
-
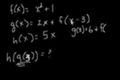 Functions Part 2
cc
Functions Part 2
ccMore examples of solving function problems
-
 Functions (Part III)
cc
Functions (Part III)
ccEven more examples of function exercises. Introduction of a graph as definition of a function.
-
 Functions (part 4)
cc
Functions (part 4)
ccAn example of a functions problem submitted by a youtube viewer
Classic function videos
These oldie-but-maybe-goodies are the original function videos that Sal made years ago for his cousins. Despite the messy handwriting, some people claim that they like these better than the new ones (they claim that there is a certain charm to them). We'll let you decide.