Khan Academy on a Stick
Multiplying and factoring expressions
This topic will add a ton of tools to your algebraic toolbox. You'll be able to multiply any expression and learn to factor a bunch a well. This will allow you to solve a broad array of problems in algebra.
-
 Factoring Special Products
cc
Factoring Special Products
ccFactoring Special Products
-
 Example 1: Factoring difference of squares
cc
Example 1: Factoring difference of squares
ccFactoring difference of squares
-
 Example 2: Factoring difference of squares
cc
Example 2: Factoring difference of squares
ccFactoring difference of squares
-
 Factoring to produce difference of squares
Factoring to produce difference of squares
-
 Example: Factoring perfect square trinomials
cc
Example: Factoring perfect square trinomials
ccFactoring perfect square trinomials
-
 Example: Factoring a fourth degree expression
cc
Example: Factoring a fourth degree expression
ccFactoring Special Products 2
-
 Example: Factoring special products
cc
Example: Factoring special products
ccFactoring Special Products 1
Factoring special products
You will encounter very factorable quadratics that don't always seem so. This tutorial will expand your arsenal by exposing you to special products like difference-of-squares and perfect square quadratics.
-
 Multiplying Monomials
cc
Multiplying Monomials
ccMultiplying Monomials
-
 Dividing Monomials
cc
Dividing Monomials
ccDividing Monomials
-
 Multiplying and Dividing Monomials 1
cc
Multiplying and Dividing Monomials 1
ccMultiplying and Dividing Monomials 1
-
 Multiplying and Dividing Monomials 2
cc
Multiplying and Dividing Monomials 2
ccMultiplying and Dividing Monomials 2
-
 Multiplying and Dividing Monomials 3
cc
Multiplying and Dividing Monomials 3
ccMultiplying and Dividing Monomials 3
-
 Monomial Greatest Common Factor
cc
Monomial Greatest Common Factor
ccMonomial Greatest Common Factor
Multiplying and dividing monomials
"Monomials" sounds like a fancy word, but it just refers to single terms like "4x" or "8xy" or "17x^2z". In this tutorial, we'll learn to multiply and divide them using ideas you're already familiar with (like exponent properties and greatest common factor).
-
 Multiplying binomials word problem
cc
Multiplying binomials word problem
ccMultiplying binomials word problem
-
 FOIL for multiplying binomials
cc
FOIL for multiplying binomials
ccFOIL method for multiplying binomials
-
 Multiplying Binomials with Radicals
Multiplying Binomials with Radicals
Multiplying Binomials with Radicals
-
 Multiplying binomials example 1
cc
Multiplying binomials example 1
ccMultiplying binomials
-
 FOIL method for multiplying binomials example 2
cc
FOIL method for multiplying binomials example 2
ccFOIL method for multiplying binomials example 2
-
 Square a Binomial
cc
Square a Binomial
ccSquare a Binomial
-
 Special Products of Binomials
cc
Special Products of Binomials
ccSpecial Products of Binomials
-
 Multiplying binomials to get difference of squares
cc
Multiplying binomials to get difference of squares
ccMultiplying binomials to get difference of squares
-
 Squaring a binomial
cc
Squaring a binomial
ccSquaring a binomial
-
 Squaring a binomial example 2
cc
Squaring a binomial example 2
ccSquaring a binomial example 2
-
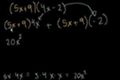 Classic multiplying binomials video
cc
Classic multiplying binomials video
cc(Ax+By)(Ax+By)
Multiplying binomials
In this tutorial you'll learn that multiplying things like (4x-7)(-9x+5) just require the distributive property that you learned in elementary school. We'll touch on the FOIL method because it seems to be covered in a lot of schools, but we don't like it (we don't think it is good to memorize processes without knowing the why).
-
 Factoring and the Distributive Property 3
cc
Factoring and the Distributive Property 3
ccFactoring and the Distributive Property 3
-
 Factoring linear binomials
Factoring linear binomials
-
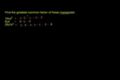 Factoring and the Distributive Property
cc
Factoring and the Distributive Property
ccFactoring and the Distributive Property
-
 Factoring and the Distributive Property 2
cc
Factoring and the Distributive Property 2
ccFactoring and the Distributive Property 2
-
 Factor expressions using the GCF
cc
Factor expressions using the GCF
ccFactor expressions using the GCF
Factoring simple expressions
You already know a bit about multiplying expressions. We'll now reverse course and look at how to think about an expression as the product of simpler ones (just like we did when we find the factors of numbers).
-
 Factoring quadratic expressions
cc
Factoring quadratic expressions
ccFactoring Quadratic Expressions
-
 Examples: Factoring simple quadratics
Examples: Factoring simple quadratics
A few examples of factoring quadratics
-
 Example 1: Factoring quadratic expressions
cc
Example 1: Factoring quadratic expressions
ccFactoring trinomials with a leading 1 coefficient
-
 Example 1: Factoring trinomials with a common factor
cc
Example 1: Factoring trinomials with a common factor
ccFactoring trinomials with a common factor
Factoring quadratic expressions
Not only is factoring quadratic expressions (essentially second-degree polynomials) fun, but it is good for you. It will allow you to analyze and solve a whole range of equations. It will allow you to impress people at parties and move up the career ladder. How exciting!
-
 Factor by Grouping and Factoring Completely
cc
Factor by Grouping and Factoring Completely
ccFactor by Grouping and Factoring Completely
-
 Example: Basic grouping
cc
Example: Basic grouping
ccFactoring Trinomials by Grouping 1
-
 Example 1: Factoring by grouping
cc
Example 1: Factoring by grouping
ccFactoring trinomials with a non-1 leading coefficient by grouping
-
 Example 2: Factoring by grouping
cc
Example 2: Factoring by grouping
ccU09_L1_T2_we2 Factoring Trinomials by Grouping 2
-
 Example 3: Factoring by grouping
cc
Example 3: Factoring by grouping
ccFactoring simple quadratic expressions
-
 Example 4: Factoring by grouping
cc
Example 4: Factoring by grouping
ccFactoring Trinomials by Grouping 4
-
 Example 5: Factoring by grouping
cc
Example 5: Factoring by grouping
ccFactoring Trinomials by Grouping 5
-
 Example 6: Factoring by grouping
cc
Example 6: Factoring by grouping
ccFactoring Trinomials by Grouping 6
Factoring by grouping
Factoring by grouping is probably the one thing that most people never really learn well. Your fate doesn't have to be the same. In this tutorial, you'll see how factoring by grouping can be used to factor a quadratic expression where the coefficient on the x^2 term is something other than 1?
Factoring quadratics in two variables
We'll now extend the application of our quadratic-factoring toolkit, by factoring expressions with two variables. As we'll see, this is really just an extension of what you probably already know (or at least will know after working through this tutorial). Onward!
-
 Terms coefficients and exponents in a polynomial
cc
Terms coefficients and exponents in a polynomial
ccTerms coefficients and exponents in a polynomial
-
 Interesting Polynomial Coefficient Problem
cc
Interesting Polynomial Coefficient Problem
ccFinding the coefficients of a third degree polynomial given 2 roots and the y-intercept
-
 Polynomials1
cc
Polynomials1
ccPolynomials1
-
 Polynomials 2
cc
Polynomials 2
ccPolynomials 2
-
 Evaluating a polynomial at a given value
cc
Evaluating a polynomial at a given value
ccEvaluating a polynomial at a given value
-
 Simplify a polynomial
cc
Simplify a polynomial
ccWorking through simplifying a polynomial
-
 Adding Polynomials
cc
Adding Polynomials
ccAdding Polynomials
-
 Example: Adding polynomials with multiple variables
cc
Example: Adding polynomials with multiple variables
ccBasic example of simplifying a polynomial expression with multiple variables.
-
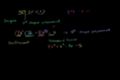 Addition and Subtraction of Polynomials
cc
Addition and Subtraction of Polynomials
ccAddition and Subtraction of Polynomials
-
 Adding and Subtracting Polynomials 1
cc
Adding and Subtracting Polynomials 1
ccAdding and Subtracting Polynomials 1
-
 Adding and Subtracting Polynomials 2
cc
Adding and Subtracting Polynomials 2
ccAdding and Subtracting Polynomials 2
-
 Adding and Subtracting Polynomials 3
cc
Adding and Subtracting Polynomials 3
ccAdding and Subtracting Polynomials 3
-
 Subtracting Polynomials
cc
Subtracting Polynomials
ccSubtracting Polynomials
-
 Subtracting polynomials with multiple variables
cc
Subtracting polynomials with multiple variables
ccSubtracting polynomials with multiple variables
Polynomial basics
"Polynomials" sound like a fancy word, but you just have to break down the root words. "Poly" means "many". So we're just talking about "many nomials" and everyone knows what a "nomial" is. Okay, most of us don't. Well, a polynomials has "many" terms. From understanding what a "term" is to basic simplification, addition and subtraction of polynomials, this tutorial will get you very familiar with the world of many "nomials." :)
-
 Multiplying Monomials by Polynomials
cc
Multiplying Monomials by Polynomials
ccMultiplying Monomials by Polynomials
-
 Multiplying Polynomials
cc
Multiplying Polynomials
ccMultiplying Polynomials
-
 Multiplying Polynomials 3
cc
Multiplying Polynomials 3
ccMultiplying Polynomials 3
-
 More multiplying polynomials
cc
More multiplying polynomials
ccMore multiplying polynomials
Multiplying polynomials
You'll see in this tutorial that multiplying polynomials is just an extension of the same distributive property that you've already learned to multiply simpler expression (that's why we think FOIL is lame--it doesn't generalize and it is more memorization than real understanding).
-
 Polynomial Division
cc
Polynomial Division
ccPolynomial Division
-
 Polynomial divided by monomial
cc
Polynomial divided by monomial
ccPolynomial divided by monomial
-
 Dividing multivariable polynomial with monomial
cc
Dividing multivariable polynomial with monomial
ccDividing multivariable polynomial with monomial
-
 Dividing polynomials 1
cc
Dividing polynomials 1
ccDividing polynomials 1
-
 Dividing polynomials with remainders
cc
Dividing polynomials with remainders
ccDividing polynomials with remainders
-
 Synthetic Division
Synthetic Division
Basic algorithm for Synthetic Division
-
 Synthetic Division Example 2
Synthetic Division Example 2
Another example of applying the basic synthetic division algorithm
-
 Why Synthetic Division Works
Why Synthetic Division Works
Demonstrating why synthetic division gives you the same result as traditional algebraic long division
-
 Factoring Sum of Cubes
cc
Factoring Sum of Cubes
ccFactoring Sum of Cubes
-
 Difference of Cubes Factoring
Difference of Cubes Factoring
u12 l2 t3 we2 Difference of Cubes Factoring
-
 Algebraic Long Division
cc
Algebraic Long Division
ccDividing one polynomial into another
-
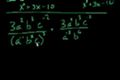 Algebra II: Simplifying Polynomials
cc
Algebra II: Simplifying Polynomials
cc17-22, simplifying polynomials and algebraic expressions
Dividing polynomials
You know what polynomials are. You know how to add, subtract, and multiply them. Unless you are completely incurious, you must be wondering how to divide them! In this tutorial we'll explore how we divide polynomials--both through algebraic long division and synthetic division. (We like classic algebraic long division more since you can actually understand what you're doing.)
 Factoring quadratics with two variables
Factoring quadratics with two variables Factoring quadratics with two variables example
Factoring quadratics with two variables example